excluding the new encrypted training abilities - is ConcreteML utilizing levelled homomorphic encryption if it’s only about encrypted inference? after training a model in clear the number of levels could be calculated and therefore leveraging the faster levelled HE or am i missing something?
Hello, thanks for the question @luu
Leveled homomorphic encryption means we have circuits without programmable bootstrapping (PBS): it means that the noise grows continuously in the circuit. PBS are the way to reduce the noise from time to time, in the circuit.
In Concrete ML, we have linear models (eg, logistic regression) which are completely leveled, ie do not have PBS. The other kind of models (tree-based models or deep learning torch-like models) have PBS.
You’re right that, when things are only linear like in linear models, it would be possible to use only partially-homomorphic encryption schemes like Paillier scheme. In Concrete ML and Concrete, we have chosen to support a single scheme (TFHE) which is able to handle all the possibilities / cases. And for linear models in Concrete ML, things are still very fast, since additions in TFHE are also not costly.
In some other libraries, they use mostly leveled circuits, ie no bootstrapping (either because they can’t or because it’s too inefficient) so it means they’ll never be able to deal with too-deep circuits. At Zama, we have chosen TFHE, which is able to deal with as-deep and as-wide neural network as we want. And it’s shown in our whitepaper that it works very well, since we have been able eg to make a NN with 100 layers.
Does it answer your question?
Hey Benoit & luu,
very informative and good question!
revising your answer @benoit every non-linear model is using PBS and therefore is Fully Homomorphic. Linear models work on leveled TFHE.
The following paper
[1906.00148] SHE: A Fast and Accurate Deep Neural Network for Encrypted Data (arxiv.org)
using leveled TFHE, therefore no PBS, but still were able to use a accurate homomorphic ReLU function and a homomorphic max pooling?
question therefore would be?
was this leveled approach for inference not better suited (no “costly” PBS needed) or did this specific approach not suit for all non-linear models (tree-based methods, other neural net activation functions)?
Hey.
I wouldn’t be able to comment too much on this paper that I don’t know well. Yes maybe there are cases where it’s possible to have faster inferences. Note however that the paper is from 2019 so there is no comparison with Concrete here.
What we tried to have with Concrete and Concrete ML was (i) simplicity for users (ii) versatility, ie it works for all cases. Which makes that, at the end, we are virtually able to deal with all circuits. So I wouldn’t be surprised that it’s sometimes possible to have faster implementation if one makes specific changes.
If you think this paper is a way to make things faster in Concrete ML: we very welcome contributions! We even have a bounty program for that, GitHub - zama-ai/bounty-and-grant-program: Zama Bounty Program and Grant Program: Contribute to the FHE space and Zama's open source libraries and get rewarded 💰, don’t hesitate ![]()
Hey Benoit, thanks a for clarifying that. I get that there is a trade-off for ConcreteML to work for a wide range of cases ![]()
Indeed. And a lot of other improvements to come! We keep improving the library, continuously, and we try to not break the APIs such that it’s regular improvements for the user, without any changes on their side.
thanks for the clarification. answered my question
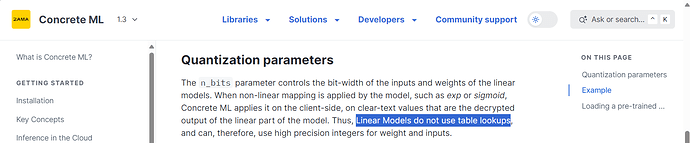
Hey Benoit, would like to note in my thesis that linear models are using leveled TFHE. Do you maybe know if that’s somewhere stated for using as a reference (documentation, source code)?
I only found this here but not sure if it’s enough to confirm the leveled approach:
Yes looks good.
Or, what you can do is to compile with show_mlir=True and look in the MLIR: you’ll see that there is no PBS here.
When the thesis is written, don’t hesitate to share it on discord.fhe.org, in # concrete or # concrete-ml channels! It may interest some people.
thanks for the fast reply! will share it once it’s done ![]()