Could somebody clarify how LUT (Lookup Table) rotation for bootstrapping works?

Zama TFHE-rs
21

well no we can choose our encoding e.g. with a padding bit always set to 0 and 2 bits we can choose to represent negative values in a similar way

000 = 0
001 = 1
010 = -2
011 = -1

q = 4 it’s just a way to see the modular representation in [-q/2; q/2[ instead of [0; q[

and if you use the padding bit, then as said earlier you map [q/2; q[ to [-q/2; 0[

000 = 0
001 = 1
010 = 2
011 = 3
100 = -4
101 = -3
110 = -2
111 = -1

q = 8

then you need to make sure you are using negacyclic luts properly which respect the encoding

I saw you asked a question here about bivariate lut Which division algorithm does Zama for TFHE?

the way it works is we concatenate things

over 2 bits to compute the AND gate for example, MSB is LHS and LSB is RHS

00 (both inputs false) => 0
01 (lhs input false) => 0
10 (rhs input false) => 0
11(both input true) => 1

then to compute the lut we do

PBS(lhs * 2 + rhs) = PBS(concat(lhs, rhs))

it is just a way to encode a lut for concatenated inputs

this generalizes to bigger inputs over more bits

00 | 11 ← this would be an LHS over 2 bits = 0 concatenated with an RHS over 2 bits = 3

and you would do PBS(lhs * 4 + rhs)

22

Thanks, your every answer is invaluable, as these pieces of knowledge can be hardly learned from elsewhere. It’ also amazing the you already know all of these flawlessly.

Regarding your explanation on division, you mean each bit is a standalone THFE ciphertext and we must build a logic circuit for binary division like this, right?
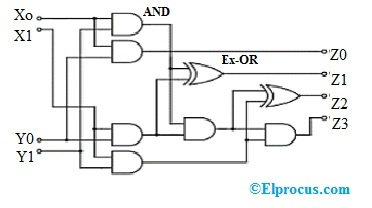
image
Is this also what Zama is doing, instead of doing division on a ciphertext as a whole number? Although other techniques like Ralph-Newton can divide a number as a whole, Zama is not using this because this is computationally inefficient?

==============

Regarding the 0 padding bit:
Case 1. if we do not use a negacyclic function, then our ciphertext’s MSB should remain to be zero, meaning that we should not rotate LUT V more than N-1 positions to the left. In this case, as we rotate V to the left by {0, 1, 2, … N-1} positions, the rotated V’s constant term coefficient will be {m_0, … m_1, … m_2, … m_{p/2 - 1} }. Here, we have repetitions between each m_{i} and m_{i+1} pair group, because we encounter for multiple noisy ciphertext states (m_i + e_{1,2,3,…} } that are mapped to the same plaintext m_i. And importantly, we should not rotate V(X) more than N-1 positions, because if we rotate V by {N, N+1, N+2, … 2N-1} positions, then the rotated V’s constant term coefficient will be {-m_0, … -m_1, … -m_2, … -m_{p/2 - 1} }, whose signs are flipped.

Case 2. On the other hand, if we use a negacyclic function, then the ciphertext’s MSB is okay to be 1. This means we are okay to rotate V(X) up to 2N positions to the left. So here I have a question. As we rotate V(X) to the left by {0, 1, … N-1} positions, the rotated V(X)'s constant term coefficients will be, like before, {m_0, … m_1, … m_{p/2 - 1} }. Then, as we continue to {N, N+1, … 2N-1} rotations, this time we will get {m_0, … m_1, … m_{p/2 - 1} }, whose negative signs are cancelled out by the negacyclic function. Note that although V(X) can have total 2N coefficient states, the latter N states are identical with the first N states (as the negacyclic function removed the negative signs). This is a problem, because now we never get the other half of plaintext states: {m_{p/2}, m_{p/2 + 1}, … m_{p-1} }. How do we get these states?

I am sorry for my continued question, but I really need to understand this correctly… I always appreciate you patient and considerate answers.

23

To be fair I have been worky daily on crypto related implementations for something like 3 years now, makes things easier to learn when you need to get them right and working :slight_smile:

division: we process things bit by bit but we could have several bits in a ciphertext, a look up table can be used to mask and extract the right bit we are interested in even if there are several in a ciphertext block(I would recommend keeping on the other post for it as it’s a whole topic on its own)

Case 1 : yes

Case 2 : the big difficulty that you just discovered is that we need a negacyclic function meaning we really have the freedom for only half of all the possible values, the negacyclic property then forces our hand for the other half but if your computations are compatible with it then you can use the full p not only p/2 which arguably is more efficient as we bootstrap more useful bits than with the padding bit = 0 but on the other hand it’s a small nightmare in itself to use, so most of the time (i.e. for now almost always) we keep the padding bit set to 0, as then the N values we have control over map exactly to the p/2 plaintext space

My pleasure

24

Thanks, I got the division part. I think I am almost understanding the whole bootstrapping now, but one small uncertain part I am concerned about is the following:

This makes sense if you are talking about programmable bootstrapping of mapping the input to the output in LUT (e.g., 011 mapped to -1).

However, do you also mean that we can represent a whole plaintext number as the above? For example, suppose we have a 4-bit plaintext and we want to compute 2 - 3, each of which will be represented as 0010 (2) and 0011 (3). If we do a binary subtraction of 0010 - 0011 = 1111 (-1), now we have 1 at the MSB. Our 0-padding scheme wanted to ensure that the MSB always stays 0. However, even if we want to encode -1 as 0111, our computer CPUs will compute 0010 - 0011 = 1111, because this is the way how our CPU and machine code are designed to do binary subtraction given the 4-bit data type. Therefore, if our application wants to use negative numbers, it seems that we will inevitably have 1 at the MSB after computations like 2 - 3 (i.e., 0010 - 0011). How can we ensure the MSB to be still 0 after such computation like 2 - 3, or 1 - 4?

==================
p.s. I think the solution is not necessarily enforcing 0 to the MSB, but enforcing the application to rotate the LUT V(X) only at most n-1 positions. This way, the application will read the constant term coefficient in V(X) only one version for each coefficient (i.e., only one-signed version, either + or -), not two versions (i.e., two contradicting signs of + and - for the same coefficient). For example, given q = 16, we can allow the application to use the following 8 plaintext numbers instead of 16 numbers:

1010: -4
1011: -3
1110: -2
1111: -1
0000: 0
0001: 1
0010: 2
0011: 3

Suppose our LUT V(X) is an 8-degree polynomial, and let’s ignore the noise (e) for now (i.e., the noise does not contribute to the ciphertext). Then, using the above 8 numbers, V(X) will be rotated to at most n-1 different positions. Therefore, we can prevent any coefficients from being reused after a sign-flip. However, for example, if our application used one more number as below:

0100: 4

Then, the polynomial V(X) can be rotated maximum 9 positions. But since it has only 8 terms, some term would be reused after its coefficient’s sign gets flipped. Then, we will get a contradicting bootstrapping map for this sign-flipping coefficient. So, we should ensure that the application uses only continous half of p values in the plaintext domain (while the MSB is allowed to be both 1 and 0). If the application abides by this, then we can avoid the negacyclic rotation problem. Is my understanding correct?

25

(x - 3) mod 4

Power of 2 should work nicely with the modulus

Or you first add the modulus then subtract to keep the proper modulus

(x + 4 - 3) mod 4

26

I am sorry, but I think I got a little lost… Is your formula (x - 3) mod 4 talking about how to implement this encoding?

You said (x - 3) mod 4, and do we plug in x={0, 1, -2, -1}? Then, we get:
x=0 : -3 mod 4 = 1 (01)
x=1 : -2 mod 4 = 2 (10)
x=-2 : -5 mod 4 = 3 (11)
x=-1 : -4 mod 4 = 0 (00)

27

Because 3 is in reality -1 with q = 4 so -3 = -(-1) = +1

If you need more help in the crypto side of things consider asking questions in the beginner channel of fhe.org discord : https://discord.fhe.org/

The community forum is more meant for usage of Zama’s products

Cheers

28

Thanks for the Discord forum which seems to be useful.

While I was working on TFHE implementations with Zama I wanted to get some of my understanding clear about the logic behind it. While I was taking my private note of summary, more questions came up, so I asked:

Thanks for all your clarifications and they were truly great advice and guidance to me.

29

Glad it was useful to you