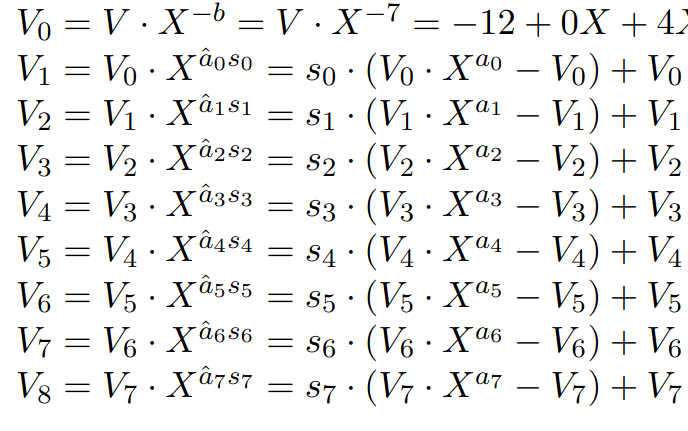Could somebody clarify how LUT (Lookup Table) rotation for bootstrapping works?

[Ronny_Ko]

Hi,

I learned about how LUT (Lookup Table) polynomial rotation works in Zama from this article:
https://www.zama.ai/post/tfhe-deep-dive-part-4

However, I am very confused about why this work…

The purpose of LUT polynomial rotation during bootstrapping is to position the value of the noise-removed plaintext value at the constant term of the LUT polynomial, so that we can extract this coefficient value homomorphically.

To illustrate this, let’s suppose the following example setup:

p = 4 // plaintext space {0, 1, 2, 3}
q = 8 // ciphertext space {0, 1, 2, 3, 4, 5, 6, 7}
m = 3 // a plaintext message
e = 1 // a noise
Delta = 2 // the scale factor, which q / p

The ciphetext is 3 bit, where as the plaintext is 2 bits. Therefore, we scale the plaintext to the left by 1 bit (i.e., multiplying by Delta=4), and reserve the smallest bit for the noise. Thus, when we decrypt the ciphertext, we will simply ignore the last bit and put 0 here (regarding it is a noise).

The following is a mapping between a noisy (Delta-scaled) plaintext and the clean (Delta-scaled) plaintext:
(Delta * m + e, Delta * m)
(0, 0)
(1, 0)
(2, 2)
(3, 2)
(4, 4)
(5, 4)
(6, 6)
(7, 6)

Given this setup, the LUT polynomial should look like this:
V(X) = 0 + X + 2X^2 + 3X^3 + 4X^4 + 5X^5 + 6X^6 + 7X^7

In V(X), each term’s exponent X^i represents the noisy plaintext “Delta * m + e”, and each coefficient c_i represents the noise-removed clean plaintext “Delta * m”.

For each case of noisy plaintext, we rotate V(X) to he left that amount. This gives us the rotation strategy like the following:

<Delta m + e = 0>

• V(X) * X^{0} = 0 + 0X + 2X^2 + 2X^3 + 4X^4 + 4X^5 + 6X^6 + 6X^7
  => The constant term’s coefficient is 0 (= Delta * m)

<Delta m + e = 1>

• V(X) * X^{-1} = 0 + 2X + 2X^2 + 4X^3 + 4X^4 + 6X^5 + 6X^6 - 0X^7
  => The constant term’s coefficient is 0 (= Delta * m)

<Delta m + e = 2>

• V(X) * X^{-2} = 2 + 2X + 4X^2 + 4X^3 + 6X^4 + 6X^5 - 0X^6 - 0X^7
  => The constant term’s coefficient is 2 (= Delta * m)

<Delta m + e = 3>

• V(X) * X^{-3} = 2 + 4X + 4X^2 + 6X^3 + 6X^4 - 0X^5 - 0X^6 - 2X^7
  => The constant term’s coefficient is 2 (= Delta * m)

<Delta m + e = 4>

• V(X) * X^{-4} = 4 + 4X + 6X^2 + 6X^3 - 0X^4 - 0X^5 - 2X^6 - 2X^7
  => The constant term’s coefficient is 4 (= Delta * m)

<Delta m + e = 5>

• V(X) * X^{-5} = 4 + 6X + 6X^2 - 0X^3 - 0X^4 - 2X^5 - 2X^6 - 4X^7
  => The constant term’s coefficient is 4 (= Delta * m)

<Delta m + e = 6>

• V(X) * X^{-6} = 6 + 6X - 0X^2 - 0X^3 - 2X^4 - 2X^5 - 4X^6 - 4X^7
  => The constant term’s coefficient is 6 (= Delta * m)

<Delta m + e = 7>

• V(X) * X^{-7} = 6 - 0X - 0X^2 - 2X^3 - 2X^4 - 4X^5 - 4X^6 - 6X^7
  => The constant term’s coefficient is 6 (= Delta * m)

So far, all things are good, because rotated constant term’s coefficient value exactly matches our expected (Delta-scaled) plaintext. This rotation works if the number of rotation positions is between 0 and 7.

However, things start to break if we rotate more than 7 positions. During the actual blind (homomorphic) rotation of LUT, we will probably end up rotating V(X) more than N(=8) times back and forth while we perform homomorphic MUX logic. Therefore, we need to ensure that the LUT works even when we rotate the table more than 8 times.

The followings are the results if we rotate V(X) between 8 and 15 positions:

8 Rotations: <Delta m + e = 0>

• V(X) * X^{-8} = -0 - 0X - 2X^2 - 2X^3 - 4X^4 - 4X^5 - 6X^6 - 6X^7
  => The constant term’s coefficient is -0 = 0 (= Delta * m = 0)

9 Rotations: <Delta m + e = 1>

• V(X) * X^{-9} = -0 - 2X - 2X^2 - 4X^3 - 4X^4 - 6X^5 - 6X^6 + 0X^7
  => The constant term’s coefficient is -0 = 0 (= Delta * m = 0)

10 Rotations: <Delta m + e = 2>

• V(X) * X^{-10} = -2 - 2X - 4X^2 - 4X^3 - 6X^4 - 6X^5 + 0X^6 + 0X^7
  => The constant term’s coefficient is -2 ≡ 6 mod 8 (≠ Delta * m = 2)

11 Rotations: <Delta m + e = 3>

• V(X) * X^{-11} = -2 - 4X - 4X^2 - 6X^3 - 6X^4 + 0X^5 + 0X^6 + 2X^7
  => The constant term’s coefficient is -2 ≡ 6 mod 8 (≠ Delta * m = 2)

12 Rotations: <Delta m + e = 4>

• V(X) * X^{-12} = -4 - 4X - 6X^2 - 6X^3 + 0X^4 + 0X^5 + 2X^6 + 2X^7
  => The constant term’s coefficient is -4 ≡ 4 mod 8 (= Delta * m = 4)

13 Rotations: <Delta m + e = 5>

• V(X) * X^{-13} = -4 - 6X - 6X^2 + 0X^3 + 0X^4 + 2X^5 + 2X^6 + 4X^7
  => The constant term’s coefficient is -4 ≡ 4 mod 8 (= Delta * m = 4)

14 Rotations: <Delta m + e = 6>

• V(X) * X^{-14} = -6 - 6X + 0X^2 + 0X^3 + 2X^4 2X^5 + 4X^6 + 4X^7
  => The constant term’s coefficient is -6 ≡ 2 mod 8 (≠ Delta * m = 6)

15 Rotations: <Delta m + e = 7>

• V(X) * X^{-15} = -6 + 0X + 0X^2 + 2X^3 + 2X^4 + 4X^5 + 4X^6 + 6X^7
  => The constant term’s coefficient is -6 ≡ 2 mod 8 (≠ Delta * m = 6)

As you can see above, half of the rotation cases give a wrong constant-term coefficient value for Delta * m. We get this problem because V(X) is a negacyclic polynomial, flipping its coefficient signs whenever they wrap around the X^0 and X^n boundary. We wouldn’t have this problem if the signs didn’t flip…

I don’t know how to come up with a Lookup Table that works. Maybe I have a wrong understanding about how we should create the mappings among the LUT polynomial’s exponents & coefficients, and the space of noisy ciphertext & plaintext?

If so, what should be the correct LUT polynomial look like in this case?

I would really appreciate it if someone come up and clarify my misconception… Thanks a lot.

[IceTDrinker]

@Ronny_Ko you are correct in saying that rotating more than the polynomial size will have a weird effect.

The polynomial ring we use is quotiented by X^N + 1 meaning that rotating more than N will result in negative values (to the negacyclic nature of the product) appearing.

This means that we need to keep the most significant bit equal to 0, we call this bit “the padding bit”, which in practice would mean that your q is twice as large and we must ensure that bit remains equal to 0 so that we don’t rotate more than N.

However if the function you apply is negacyclic then you can make use of the 2N possibilities of the look up table.

Hope that helps

[Ronny_Ko]

Thanks very much for your quick answer. I really appreciate this.

Q1. I think I didn’t fully understand what you said… You said that we add an extra padding bit at the MSB and ensure to keep this bit to remain zero during the blind rotation (i.e., ensuring that we do not rotate more than N). However, I think this is not possible, because we have no idea how many positions each stage of rotation make, because the rotation is done in a blind manner, so we do not know what is the value of the MSB of each coefficient after each stage of rotation. Most likely, I think we would end up rotating the V polynomial more than N or 2N times to either direction, while we do these multiple steps of polynomial homomorphic multiplications:

Q2. I understand that in a negacyclic polynomial, there can be maximum 2N distinct coefficient states during rotations. However, having 2N distinct coefficients instead of N does not seem to help us at all, because actually we have this weird problem because we have the other N sign-flipping coefficients. We cannot really use the other N sign-flipping coefficient states, I think. But you said “you can make use of the 2N possibilities of the look up table”. Then, how can I use the full 2N encodings during the rotation? Is there a separate data structure called a look up table besides the V polynomial? Is it that a separate look up table has mappings between the LWE-encrypted coefficient values of V (total maximum 2N such ciphertext values) and their mappings to another 2N sets of LWE-encrypted values that encrypts the actual Delta*m plaintexts (total p distinct such values)? If there is such a pre-defined dictionary between ciphertexts, this looks like an electronic code book (in AES-ECB) which would leak plaintext access patterns.

I wonder if it could be possible to clarify my misunderstanding by using an actual example of V and rotation examples with actual ciphertexts and the underlying plaintexts… I am sorry if this is cumbersome to you, but walking through an actual example would really help a lot. I am having this understanding difficulty because there was no actual example of rotation bootstrapping in the description webpage.

[IceTDrinker]

So we must ensure that the corresponding decrypted plaintext has the MSB/padding bit set to 0 then the rotation works ok, I can tell you because that’s what we use at Zama all the time I’m not a cryptographer but the idea is that while doing the rotation in the end as we perform the decryption then the value that matters in the padding bit is the equivalent decrypted value and we can manage that as we know our inputs and the circuit we execute

as for the N vs 2N thing, if the function is negacyclic we can fully define it with N values, the N high values are “just” the negated low values

if the function is not negacyclic we end up using the N values and we cannot use the negated ones if we have a padding bit != 0

[Ronny_Ko]

I see, so you mean after the end of rotation, is it that you extract the LWE ciphertext located at the constant position of the polynomial V and then you decrypt it to check the MSB’s value whether it is 1 or 0? But this LWE ciphertext is encrypted with the secret key S, thus the server cannot decrypt it unless the data owner gives his/her key S to the server. The purpose of bootstrapping was to reduce the noise in a ciphertext without fully decrypting it.

Also, even if you know the MSB value, how do you ensure that this bit does not become 1? During bootstrapping, after the modulus switch, the ciphertext space gets reduced from q to 2n. This means that some ciphertext values would require the polynomial to be rotated more than n positions at a certain rotation stage, in which case all coefficients in the polynomial V would make more than a full-round rotation.

It there were a walk-through example, it would be easier for me to understand…

[IceTDrinker]

we don’t decrypt on the server side, the math guarantee that IF you decrypted, the MSB would be 0 if you made sure it was zero for your circuits and inputs.

You may have missed the fact that there is a modulus switch before the PBS going from q to 2N which introduces a lot of noise, but again for the right parameter choice that noise won’t change the PBS result

[Ronny_Ko]

Thanks, I think I got more clear understanding now. So, given our following ciphertext layout (size of q):

… during our homomorphic computations (e.g., add, multiply), we need to ensure that the MSB bit should always stay 0, right? If the MSB of a ciphertext is 0, then the number of blind rotation positions as the exponent of X (where V(X)*X^-{\Delta * m + e}) is mathematically guaranteed to be less than N (i.e., it will be at most N - 1).

If this is correct, then I got this part. But the question is, how can we enforce that the MSB of a ciphertext (of size q) stays 0? By structure of the encryption scheme, every bit of the ciphertext is uniformly random. Therefore, if we continue many homomorphic computations, the MSB of the ciphertext will be sometimes 0 and sometimes 1 (with 50% chances). Given this, how can we enforce the MSB to stay 0 across homomorphic encryption, addition, and multiplication?

[IceTDrinker]

That’s the padding bit role, it’s only meaningful when considering the equivalent plaintext, of course there is randomness on top of that bit, but as long as the underlying plaintext has a 0 padding bit then everything will work ok

[Ronny_Ko]

Thanks, now it makes much better sense to me. So basically, we should design our circuit (or our use case system) such that the plaintext will never have 1 in its MSB, otherwise our bootstrapping will get corrupted, right? Then does this mean that we cannot compute negative numbers by using each ciphertext as a whole number?

Another question is, you said if an n-degree plynomial LUT is negacycle, then we can encode 2N numbers. However, we cannot use such a negacyclic polynomial to encode a modulo domain. This is because for a modulo domain we need continuously wrapping series of number. For example, if q = 8, we should have the modulo domain: {0, 1, 2, 3, 4, 5, 6, 7}, then we cannot just encode V as:
V = 0 + 1X + 2X^2 + 3X^3, because rotating this polynomial gives a different number sequence: {0, 2, 3, 0, 3, 2, 1}. With this sequence of numbers, we cannot implement the modulo 8 domain. So, even if we have a negacyclic polynomial, we still need to ensure that the plaintext’s MSB is used as a padding. Is this correct?

[IceTDrinker]

So the first part is correct we have to make sure the padding bit is 0, it requires good knowledge of what you are doing or tools, like our shortint API which will make sure that padding bit stays at 0 (unless you use unchecked ops but that should only happen if you know what you are doing).

For the negative numbers I encourage you to look at 2’s complement encoding of integers : Two's complement - Wikipedia

As for the last question you can manage the modulus as long as the function is negacyclic, meaning you cannot use any function, only negacyclic ones, it may not be suitable for certain use case, because as you don’t know the content of the padding bit you can never rely on the fact it’s 0 and so need to always have negacyclic function that can work with that padding bit being 1 or 0 without being known in advance

[Ronny_Ko]

So the magic I don’t understand about a negacyclic polynomial is how it can actually handle the padding bit. Of course, if the negacyclic polynomial’s degree is 4, it can encode 4 positive coefficients and 4 negative coefficients, total 8 different numbers. However, the reason why it cannot implement a modulus is because if we rotate the polynomial coefficient passing the boundary between X^0 and X^n, it suddenly becomes negative, which breaks the modulus sequence we want.

In the example of a 4-degree polynomial V, we ideally want its rotations give the following outputs in order for us to implement a modulus 8 domain {-4, -3, -2, -1, 0, 1, 2, 3}:
0 left-shift: The constant coefficient should be 0
1 left-shift: The constant coefficient should be 1
2 left-shift: The constant coefficient should be 2
3 left-shift: The constant coefficient should be 3
4 left-shift: The constant coefficient should be -4 (≡ 4 mod 8)
5 left-shift: The constant coefficient should be -3 (≡ 5 mod 8)
6 left-shift: The constant coefficient should be -2 (≡ 6 mod 8)
7 left-shift: The constant coefficient should be -1 (≡ 7 mod 8)

This way, as we increase the rotation counts infinitely, the output coefficient will wrap around like this: 0, 1, 2, 3,-4, -3, -2, -1, 0, 1, 2, 3, -4, -3, -2, -1, … (These are the correct number-wrapping sequence of modulo 8)

But in reality, such a 4-degree negacyclic polynomial does not exist. In reality, we have this kind of polynomial V:

V = 0 + X + 2X^2 + 3X^3

As we left-shift 5~8 positions, the corresponding coefficient values should be a negative of those at left-shift 0~4. In the above example, if the left-shifts 0~4 gave the coefficient values 0,2,3,4, then the left-shifts 5~8 will give -0, -1, -2, -3. This is not -4,-3,-2,-1, which we wanted to implement the modulus 8. In other words, it would give the following outputs:
0 left-shift: The constant coefficient is 0
1 left-shift: The constant coefficient is 1
2 left-shift: The constant coefficient is 2
3 left-shift: The constant coefficient is 3
4 left-shift: The constant coefficient is -0 (Wrong)
5 left-shift: The constant coefficient is -1 (Wrong)
6 left-shift: The constant coefficient is -2 (Wrong)
7 left-shift: The constant coefficient is -3 (Wrong)

If we continue the rotation, the output coefficient will have the following broken sequence: 0, 1, 2, 3, 0, -1, -2, -3, 0, 1, 2, 3, -0, -1, -2, -3, …
These are not the correct wrapping number sequence of modulus 8.

If we have a different polynomial like this:
V = 1 + 2X + 3X^2 + 4X^3

Rotating this still does not give use the correct modulo 8 sequence:
1, 2, 3, 4, -1, -2, -3, -4, 1, 2, 3, 4, … (This number sequence does not wrap around 8 consecutive numbers)

I wonder if you could give a simple working example of 4-degree negacyclic polynomial that can successfully implement modulo 8. (Or even modulo 4).

[IceTDrinker]

This does not mean it’s broken it means the Identity LUT, i.e. [0, 1, 2, 3] is not a negacyclic function

[Ronny_Ko]

It says that the definition of a negacyclic polynomial is that a cyclic s hift of its coefficients, where the leading coefficient moves to the constant term and is negated, still results in a polynomial within the same system or ring, adhering to the ring’s operations and rules. Thus, in case of

V(X) = 0 + 1X + 2X^2 + 3X^3 in Z_8[ X ] / (X^4 + 1), where Z_8 = {-4, -3, -2 ,-1, 0, 1, 2, 3}

All of its 2N = 8 possible shifts belong to the same polynomial ring:
[0, 1, 2, 3]
[1, 2, 3, 0]
[2, 3, 0, -1]
[3, 0, -1, -2]
[0, -1, -2, -3]
[-1. -2. -3, 0]
[-2, -3, 0, 1]
[-3, 0, 1, 2]

Also in case of V[ X ] = 1 + 2X + 3X^2 + 4X^3, all the following 2N=8 possible shifts are in the same polynomial ring:
[1, 2, 3, 4]
[2, 3, 4, -1]
[3, 4, -1, -2]
[4, -1, -2, -3]
[-1, -2, -3, -4]
[-2, -3, -4, 1]
[-3, -4, 1, 2]
[-4, 1, 2, 3]

Nonetheless, their constant-coefficient terms do not give our desired modulo-8 rotation sequence of {-4 -3, -2, -1, 0, 1, 2, 3, -4, -3, -2, -1, 0, 1, 2, 3, …}

The first V(X) gives the rotation sequence {0, 1, 2, 3, 0,. -1, -2, -3, …}
The second V(X) gives rotation sequence {1, 2, 3, 4, -1, -2, -3, -4}

What V on earth can correctly encode modulo 8 when it is rotated, given Z_8 = {-4, -3, -2, -1, 0, 1, 2, 3}? Could there be just one example by any chance…?

[IceTDrinker]

well the link you shared TFHE Deep Dive - Part IV - Programmable Bootstrapping indicates that the sign function they evaluate ctrl + F sign or negacyclic is negacyclic and returns either q/8 for positive values and -q/8 for negative values

for a given N

any f such that f(x + N) = -f(x) is negacyclic

[Ronny_Ko]

Yes, the link indeed explains an AND logic gate’s bootstrapping and this makes sense. However, I wonder if there is any one example that works for a number domain instead of a bit-wise binary domain.

The link’s example works because its plaintext has only 2 states: + and -, and it placed the + part in the positive side of the negacyclic polynomial rotation, and - to the other side. That’s why it works so easily. But if the plaintext has more than 2 states, how LUT actually works?

The link’s article explained everything about TFHE assuming that the plaintext m is a number in a large number ring, like Z_8 or even Z_1024, but I failed to come up with a working LUT polynomial that would work for a number domain.

I spent a week to understand how LUT would work for a number domain (even for simple p=4, n=4, q=8 is fine), but failed to come up with a working LUT polynomial example…

[IceTDrinker]

See https://eprint.iacr.org/2021/1402.pdf

Ctrl + f negacyclic it breaks things down, a lot of functions are negacyclic and should work for « number domains » they are not necessarily useful and in practice for power of 2 moduli at least in TFHE-rs uses exclusively LUTs with the assumption that the padding bit is 0

Maybe the bit you are missing is needing to map

[q/2; q[ to [-q/2; 0[

[Ronny_Ko]

Thanks very much, now I understood. In your link, the LUT with programmable bootstrapping is as follows:

V(X) = f(0)X^0 + f(1)X^1 + … + f(n-1)X^{n-1}

, where f(z) is a programmable function.

If we want to use the entire range [0, p-1) for \mu, then f(z) should work as follows:

• If the rotation count ‘r’ of V(X) is within 0 <= r mod 2n < n, then f(z) returns z
• If the rotation count ‘r’ of V(X) is within n <= r mod 2n < 2n, then f(z) returns -z (in order to cancel out the sign-flipping side effect of rotating Z(X) ).

Importantly, f(z) should be a homomorphically computable logic (e.g., homomorphic addition, homomorphic multiply), because we are assuming to do blind rotation during bootstrapping. I wonder if my understanding is correct.

===========
My Proposed Alternative Solution
And as a another solution besides using the negacyclic function, I wonder if the following works:

Let’s define a new n-degree function f as follows whose coefficient is 1 for all terms:

f(Z) = 1 + 1X + 1X^2 + … + 1X^{n-1}

Step 1. During bootstrapping, when we rotate V(X) by r positions (where r = \rescaledDelta * m + e), we also rotate f(Z) by r positions.

Step 2. We extract the constant position’s coefficient V(X).

• If 0 <= r mod 2n < n, then we must have extracted LWE(\delta * m)
• If n <= r mod 2n < 2n, then we must have extracted LWE(-\delta * m), due to the weird (negacyclic) coefficients behavior we get when rotating V(X).

Step 3. We also extract the constant position’s coefficient f(X).

• If 0 <= r mod 2n < n, then we must have extracted LWE(1).
• If n <= r mod 2n < 2n, then we must have extracted LWE(-1).

Step 4. We homomorhically multiply the outputs of Step 2 and Step 3.

• If 0 <= r mod 2n < n, then we get LWE(\delta m) * LWE (1) = LWE(\delta * m * 1) = LWE(\delta * m)
• If n <= r mod 2n < 2n, then we get LWE(-\delta m) * LWE (-1) = LWE(-\delta * m * -1) LWE(\delta * m)

Therefore, if we multiply rotated V(X)'s constant-term coefficient with that of f(Z), then the negative signs cancel out when n <= r mod 2n < 2n, thus we are always guaranteed to get LWE(\delta m), which can eliminate the sign-flipping problem.

Do you think my solution works?

[IceTDrinker]

Strictly the function can be anything that can be expressed as a look up tavle, the result will have a flipped sign if the padding bit was 1, depending on your use case it is not desirable and in practice again we don’t do that in TFHE-rs

Only issue with your second solution is that you need two PBS one for the function, one for the sign but most importantly the homomorphic multiplication between 2 LWEs is not defined as they both represent an element of the torus and multiplication is not defined between two torus element, there are tricks to compute the multiplication nonetheless but they are expensive and as one of them uses PBSes it just might not work because of the padding bit not being 0

All that to say that we can sometime use the negacyclic property of the PBS as a trick but most of the time, at least for now, we side step the problem and just use the N usable values of the LUT when the padding bit is 0

[Ronny_Ko]

I see, so using a padding bit is the most practical solution. But if you use a padding, I still wonder how you would deal with negative numbers. Last time you showed a link about two’s complement, but I didn’t get how this can be a solution if we have to do some subtractions that would result in negative values, like:

2 - 3

The result will be -1, which is 11 in the two-bit world (e.g., Z_4). If we assume all data types are unsigned values, then 2 - 3 will be 3, which is again 11 in the two-bit world. If we subtract numbers, there are cases where the MSB will be 1. How do you handle this example’s case?

[Ronny_Ko]

The link you shared Two's complement - Wikipedia says:

When the most significant bit is 1, the number is signed as negative; and when the most significant bit is 0 the number is signed as positive.

Thus, if we enforce an application not to use the MSB as 1, this means we will have to give up using negative numbers.

Other available options of using MSB (for both 0 and 1) are implementing a bit-wise logic circuit, or piping the output of LUT to a negacyclic function.

Is my reasoning correct?