Hi,
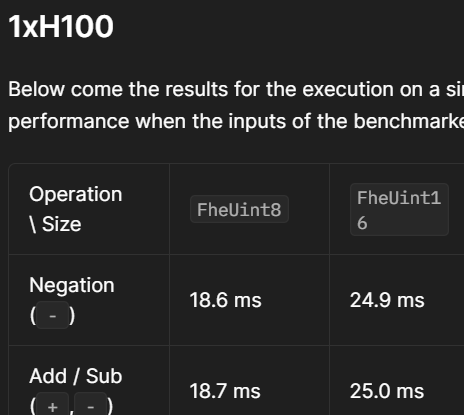
I wonder why TFHE addition (FheUint16) takes as much as 25 ms when using GPU:
https://docs.zama.ai/tfhe-rs/guides/run_on_gpu#benchmarks
Basicaly, a TFHE ciphertext is (vector(a), b). When we add two TFHE ciphertexts as follows:
C1 = (vector(a1), b1)
C2 = (vector(a2), b2)
We only need to compute C1 + C2 = (vector(a1) + vector(a2), b1 + b2)
Provided the vector is around 1000 dimension (for 128 bit security?), this computation can be done almost instantly. But the benchmark page shows that this operation takes 25 ms. I wonder why it takes so long. Is this because TFHE-rs implements a logic gate to compute addition of two ciphertexts and the multiplication operations in the gates takes a long time?
In fact, the only operation my application needs is programmable bootstrapping (switching 0 to 1, and switching all non-zero values to 0), and addition. In this case, there is no need to implement a logic gate. If this is the case, would there be any way for me to expedite the addition operation by using TFHE-rs without manually implementing my custom TFHE addition logic?
Hello, It’s not that simple:
The FheUintX/FheIntX types are actually multiple LWE
So they are:
C1 = (vector(a1), b1, ...., vector(an), bn)
C2 = (vector(a1), b1, ...., vector(an), bn)
Thus, PBS are needed to manage carries.
It is theoretically possible to encode 16 bits on a single LWE, but you need to find the parameters (we don’t provide them)
And although I think it is possible to find parameters that works for doing simple Lwe add, I’m not sure there are parameters that exist and allow to compute PBS on LWEs that encode 16 bits.
Or if they exists the runtime of the PBS would be exetremly slow: a 6 bits PBS is 100 ms, 8 bit PBS is already 800ms (the jump between the two is quite big, so 16 bits would be far worse).
This is why we represent integers using multple LWE, as we want to allow generic application to work, and be able to expose types that encrypts more than just a few bits efficiently.
I you want to try to use lower level construct in hope to achieve better performance for your specific program you would have to stick to core_crypto/shortint APIs which stay at the LWE level, or you could try the integer api but you would have to use unchecked_ operations like unchecked_add but again you’d have to be carefull about noise and carry management.
Hi, thanks very much for your clarification. PBS for 16-bit numbers (without using circuits) seems to be taking many hours… So, Zama’s strategy is to express all software logic as either a circuit composed of logic gates, or express as PBS, right?
Thanks for your insight and I will come up with an alternative way to tackle this problem.
